خوانش ریاضیاتی اخلاق اسپینوزا

معرفت‌شناسی ریاضی در افلاطون و ارسطو
همۀ هنرها و دانش‌هایی که با طبیعت سروکار دارند، در قلمرو پندار واقع می‌شوند و چون پندار معرفت نیست، درنتیجه همۀ دانش‌هایی که با طبیعت سروکار دارند، مصداق معرفت نخواهند بود، و این از آن جهت است که متعلق این دانش‌ها همواره درحال دگرگونی است و هرگز به یک حال نبوده و در آینده نیز نخواهد بود.
اگر چنین است پس معرفت را در کدام دانش باید جستجو نمود؟ افلاطون ریاضیات را پیشنهاد می‌کند. از نظر افلاطون در ریاضیات خصوصیتی وجود دارد که آن را در مرتبه‌ای بالاتر از سایر دانش‌ها قرار می‌دهد. (انتظام ۱۳۷۹)
همچنین انتظام به نقل از جمهوری افلاطون می‌نویسد:
چون ریاضیات زنجیر پندار را از پای روح آدمی برمی‌دارد و تفکر را در او برمی‌انگیزد در مرتبه‌ای بالاتر از پندار قرار داشته و نباید آن را نیز پندار بنامیم. از اینرو افلاطون نام دیگری برای آن پیشنهاد می‌کند و آن، «شناسایی از راه استدلال» است.
سپس همانطور که می‌دانیم تأکید و پافشاری دکارت در تأسیس نظام معرفتی مبتنی بر ریاضیات و اصول تردیدناپذیر، همان چیزی است که نقطۀ عطف عصر خردگرایی غربی گردیده است؛ چیزی که در میان اندیشمندان به «اصالت ریاضیات دکارت» مشهور است. گرچه گاه بنظر می‌آید که برخی دیدگاه‌ها نسبت به ریاضیات افراطی باشد اما کلیت بحث چیزی نیست که بتوان در صدق آن تردید نمود.
در ریاضیات دو ویژگی وجود دارد که امکان ایجاد معرفت و بصیرت ریاضیاتی را فراهم می‌آورد.
۱. ساختار منطقی و استنتاجی ریاضیات
۲. خاصیت مجرد بودن ریاضیات
جیمز استوارت ریاضیدان می‌گوید: «خاصیت مجرد بودن ریاضیات باعث قدرت آن شده است. یک مفهوم مجرد ریاضیاتی می‌تواند تعابیر مختلفی در علوم متفاوت داشته باشد. وقتی خواص ریاضیاتی را یک‌بار و برای همیشه درک نماییم آنگاه می‌توانیم تمام نتایج آن را در کلیۀ علوم بکار بریم. این موضوع خیلی کارآمدتر خواهد بود تا اینکه خواص مفاهیم هر علم را بطور جداگانه پیدا کنیم. بسیاری از کاربردهای مفاهیم ریاضی، به توانایی ما در استنتاج حقایق از این مفاهیم بستگی دارد.
چگونگی ایجاد معرفت ریاضی
باید دانست که معرفت ریاضی نه بیان قوانین علمی در علومی نظیر فیزیک و شیمی بلکه معرفتی است که از خود مفاهیم، و ساختارهای ریاضی و بدین‌ترتیب، توسط شناخت روابط ریاضی حاکم بر پدیده‌ها حاصل می‌گردد. اکنون به ارائۀ الگوریتمی می‌پردازیم که مراحل دستیابی به این نوع معرفت را برای ما روشن می‌سازد.
الگوریتم دستیابی به معرفت ریاضیاتی
۱. فهم محتوای مفهوم ریاضی: بازخوانی یک مفهوم خاص ریاضیاتی به این نحو که این مفهوم با توجه به ویژگی‌های خاصی که دارد، چه مفهومی را بیان می‌کند؟ یا این مفهوم چه معنای جدیدی را خلق می‌کند؟
۲. درک روابط حاکم بر اجزای مفاهیم: درک ساختار مفهوم با توجه به ساختار، اجزاء و روابط
۳. درک ارتباط این مفهوم با سایر مفاهیم: این مفهوم چه رابطۀ منطقی با سایر مفاهیم دارد؟
۴. بسط معرفتی یک مفهوم به سایر مفاهیم: اینکه با درک این مفهوم به درک چه مفاهیم و حقایقی می‌توان دست یافت؟

دو مفهوم مهم ریاضیاتی در کسب معرفت
۱. جنبۀ معرفتی مفهوم تابع
۲. جنبۀ معرفتی نظریۀ گراف‌ها

۱-جنبۀ معرفتی مفهوم تابع
گزاره و گزاره‌نما
اکنون در ادامه، به معرفی گزاره و گزاره‌نما یا تابع که مفاهیم مهمی در اثبات یا رد امور فلسفی شمرده می‌شوند می‌پردازیم:
۱. گزاره
فرض کنید به شما گفته شده است که امروز هوا ابری است. این عبارت، یک جمله خبری است که می‌توانید صحت آن را بررسی کنید. کافی است نگاهی از پنجره به بیرون بیاندازید تا درستی این ادعا را بررسی کنید. به این ترتیب به نظر می‌رسد که جمله «امروز هوا ابری است» که یک گزاره است، گزارۀ صادقی است. حال جمله «به‌به! چه هوای مطلوبی است» را در نظر بگیرید. ممکن است مطلوبیت از نظر یک فرد، آفتابی‌بودن و از نظر فرد دیگری بارانی‌بودن باشد. در نتیجه تعیین درستی یا نادرستی این عبارت برای همه افراد یکسان نبوده لذا نمی‌توان آن را یک گزاره دانست. عبارات یا جملات خبری که ارزش درستی آنها براساس اصول منطق قابل تعیین باشند، گزاره نامیده می‌شوند. گزاره‌ها معمولا با حروف p ، q و r نشان داده می‌شوند. در «منطق ارسطویی» (Aristotelian Logic) ، ارزش هر گزاره به صورت صحیح یا غلط ارائه می‌شود.

۲. گزاره‌نما یا تابع
اگر سنجش صحت یک جملۀ خبری، به یک یا چند پارامتر بستگی داشته باشد که در حال حاضر مشخص نیستند، آن عبارت یا جمله یک گزاره‌نما نامیده می‌شود. به این ترتیب، به نظر می‌رسد که گزاره‌نما، بسیار نزدیک به گزاره باشد که در حقیقت هم همینطور است. اگر مقدار دقیق پارامتر یا پارامترهای یک گزاره‌نما تعیین شوند، آنگاه آن گزاره‌نما تبدیل به یک گزاره خواهد شد. مفهوم گزاره‌نما یا تابع یکی از مهمترین و اساسی‌ترین مفاهیم پایه در ریاضیات جدید است. شکل ساده و کلی تابعِ تک‌متغیره بدین صورت است: y=f(x) . برای مثال عبارتی مانند «عدد x زوج است» را در نظر بگیرید. این عبارت یک گزاره‌نما است، زیرا بدون دانستن مقدار x، امکان ارزش‌گذاری برای این عبارت وجود ندارد؛ اما به محض مشخص شدن x ، مثلاً (x=2) گزاره‌نما تبدیل به گزاره شده و صحت آن قابل بررسی می‌شود. معمولاً گزاره‌نمای تک‌پارامتری را بصورت p (x) نشان می‌دهند؛ اما تعداد پارامترهای یک گزاره‌نما ممکن است برابر با n باشد، که در این حالت می‌نویسیم p (x1، x2،…، xn) .
اصول متعارف و اصول منطق
قوانین و گزاره‌هایی که به نظر می‌رسد در همه حالات صحیح بوده و همۀ افراد بشر در صحت آن‌ها اتفاق‌نظر دارند، اصول متعارف یا Axioms نامیده می‌شوند. با استفاده از اتفاق‌نظری که روی اصول وجود دارد، قضایا و عبارات دیگر، ارزیابی، اثبات، و یا رد می‌شوند. اگر ارتباط بین گزاره‌ها و اصول، به‌درستی برقرار شده و براساس اصول منطق باشند، در صحت قضایای حاصل تردید نخواهیم داشت. به روش‌های ارزش‌گذاری گزاره‌ها، اصول منطق گفته می‌شود؛ اصولی که همۀ افراد بشر بر آن توافق دارند. و از آنجایی که به آن‌ها اصول گفته می‌شود، احتیاج به اثبات نداشته و هر عقل سلیمی، درستی آنها را درک و استنباط می‌کند. و همانطور که می‌دانیم جملات و قضایای ریاضی در منطق به زبان گزاره‌ها‌ و سورهای منطقی بیان می‌شوند.
سور و انواع آن
برای تبدیل یک گزاره‌نما (که توضیح آن در بالا داده شد) به گزاره، از سور‌ها کمک می‌گیریم. در زبان عربی، سور به حصار دور شهر گفته می‌شود که آن را از بقیه قسمت‌ها جدا می‌کند. در منطق نیز، سور باعث می‌شود که دامنۀ یک گزاره‌نما محدود شده و با استفاده از مقدارهایی خاص، گزاره‌نما تبدیل به یک گزاره شود. در این حالت گزاره را گزاره سوری می‌نامند. استفاده از سورها باید به دقت انجام شود، زیرا قصدد اریم که براساس آن‌ها، گزاره‌نما را به یک گزارۀ درست، تبدیل و مجموعه‌جواب گزاره‌نما را بیابیم.
در این نوشتار به معرفی دو نوع سور می‌پردازیم که می‌توانند برای معرفی معیار تعهد هستی‌شناختی مفید واقع شوند: سور کلی universal quantifier ، و سور وجودی existential quantifier .
سور عمومی
اگر بخواهیم برای تبدیل یک گزاره‌نما به گزاره، از همه مقدارهای دامنه استفاده شود، از سور عمومی استفاده می‌کنیم. سور عمومی در ریاضیات به صورت ∀ نشان داده می‌شود که معکوس حرف اول عبارت انگلیسیAll است. فرض کنید گزاره‌نمای p(x) به صورت « است زوج x » نوشته شده باشد. بنابراین می‌توان آن را با سور عمومی تبدیل به یک گزاره کرد و اینطور نوشت:

∀x∈N;x>0

این عبارت به صورت: «به ازاء همۀ x های متعلق به اعداد طبیعی، x بزرگتر از صفر است» خوانده می‌شود. همچنین ممکن است آن را به صورت «برای هر عدد طبیعی x ، می‌توان نتیجه گرفت، x بزرگتر از صفر است» خواند. اگر دامنۀ این گزاره‌نما یعنی D، اعداد طبیعی در نظر گرفته شود، ارزش گزارۀ حاصل به‌ازای همۀ اعضای دامنه، درست خواهد بود. یعنی ارزش گزاره‌ای با سور کلی، زمانی درست است که دامنۀ تعریف‌شده برای گزاره‌نما با مجموعه‌جواب برابر باشد، به‌عبارت دیگر، همۀ اعضای دامنه در گزاره‌نمای p(x) صدق کنند.
سور وجودی
اگر بخواهیم نشان دهیم که به ازاء بعضی از مقدارهای دامنه، گزاره‌نما به یک گزاره تبدیل می‌شود، از سور وجودی استفاده می‌کنیم. در ریاضیات سور وجودی را به صورت ∃ نشان می‌دهند که مانند تصویر آینه‌ای حرف اول کلمه Existبه معنی وجود است. فرض کنید می‌خواهیم بیان کنیم که بعضی از مقدارهای اعداد حقیقی (R) از ۳ بزرگتر هستند. در این حالت گزاره‌نما را به صورت p(x) ∶x-3>0 مشخص کرده و به کمک سور وجودی، آن را به یک گزاره تبدیل می‌کنیم. در این حالت می‌توان نوشت:

∃ x ∈R;x-3>0

با توجه به تعیین علامت نامعادله یا نامساوِی داده شده، فقط x>3 گزاره‌نما را به یک گزاره با ارزش درست تبدیل می‌کند. بنابراین با توجه به اینکه دامنه گزاره‌نما، در این حالت اعداد حقیقی است، می‌توان گفت، زمانی ارزش گزاره سور وجودی صحیح است که مجموعه‌جواب گزاره‌نما، زیرمجموعه‌ای از دامنۀ تعریف‌شده در گزاره‌نما باشد. یعنی بعضی از اعضای دامنۀ تعریف‌شده بتواند گزارۀ سور وجودی را به گزاره‌ای با ارزش درست تبدیل کند. به بیان دیگر، اگر مجموعه‌جواب گزارۀ سور وجودی غیرتهی باشد، آنگاه آن گزاره دارای ارزش درست است.
معرفت ریاضی در نظریۀ گراف‌ها
گِراف یا نِگار در ریاضیات دست‌کم دارای دو معنی است. در ریاضیات پایه، گراف اشاره به نمودار تابع دارد، و در اصطلاح ریاضی‌دانان، گراف مجموعه‌ای از نقاط و خطوط به هم پیوسته است که اشاره به یکی از انواع نمودار تابع دارد. یک گراف از مجموعه‌ای غیرخالی از اشیاء به نام رأس تشکیل شده که با V نشان داده می‌شود و مجموعه‌ای شامل یال‌ها که رأس‌ها را به هم وصل می‌کنند و با E نان داده می‌شود. در نتیجه گراف را با G=(V، E) نشان می‌دهیم. برای بیان ارتباط میان دو مجموعۀ E و V با گراف G=(V،E) ، آنها را بصورت E(G)و V(G) نشان می‌دهند. این دو مجموعه را بصورت زیر در نظر می‌گیریم (بابلیان, ۱۳۸۶):

V={v1، v2،…، vn}   ، n∈N   ، V≠∅
E={e1، e2 ،…، em}   ، m∈N

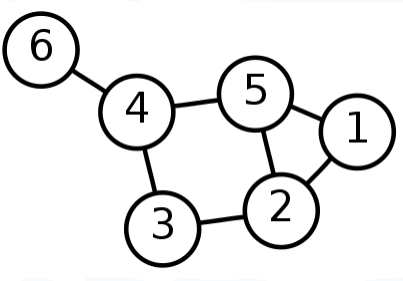
پاسخ به پرسش «چه چیزهایی در جهان وجود دارند؟ (هستی‌شناسی)» بوسیلۀ تابع ریاضیاتی و گراف
یکی از پرسش‌های بنیادینی که در زمینۀ هستی‌شناسی انسان و جهان مطرح است این است که اصولاً چه چیزهایی در جهان یا در عالم وجود دارند؟ به لیستی که توسط یک نظریۀ خاص، برای معرفی اشیائی که در عالم تحقق دارند/ وجود دارند/ واقعاً وجود دارند ارائه می‌شود، «هستی‌شناسی» یک نظریه گفته می‌شود. بعبارتی، یک نظریه با ارائۀ دیدگاه خود دربارۀ چیزهایی که در عالم وجود دارد، طرفداران خود را ملزم و متعهد و پایبند به باور به وجود آن اشیاء یا هویت‌ها، یا چیزها می‌کند. در نگاه اول می‌توان گفت که جهان تشکیل شده است از انسان، حیوان، گیاه و … . سپس می‌توان اقلام بشرساخته و مصنوعی را نیز به این فهرست افزود: کیف، کتاب، دیوار و غیره. همچنین، در این زمینه، شاید کسی بپرسد که آیا خاصیت چیزها هم باید به این فهرست افزوده شود یا خیر؟ چیزهایی نظیر جاذبه، اصطکاک، اینرسی، و غیره. دربارۀ اعداد، رویدادها، و زمان‌ها چطور؟ (Okrent, 1998)
دشواری پاسخ به اینگونه پرسش‌ها زمانی روشن‌تر می‌شود که به این موضوع فکر کنیم که اگر فقط اشیاء را موجود در جهان بدانیم، آنگاه باید وجود خواصی که در میان این اشیاء وجود دارد، بعنوان نمونه جاذبه، را رد کنیم. ولی اگر خواص این اشیاء را هم در فهرست اقلام موجود در جهان ذکر کنیم، آنگاه در عینی نشان دادن آنها توسط حواس پنجگانه به مشکل برمی‌خوریم. همچنین است دربارۀ احساسات و عواطف انسان‌ها.
از اینروست که معیار تعهد هستی‌شناختی تبدیل به یکی از محوری‌ترین و مناقشه‌برانگیزترین موضوعات حیطۀ فرامتافیزیک شده است. یعنی یک دیدگاه یا نظریۀ خاص ناظر به جهان، در تعیین هستی‌شناسی خود چه معیاری دارد. در میان آراء متعدد، دیدگاه کواین منطق‌دان و فیلسوف امریکایی را می‌توان قول مشهور دانست. وی درباب کشف تعهد هستی‌شناختی یک نظریه، فرآیندی سه‌مرحله‌ای به شرح زیر را بیان نمود (سیدی فرد & آیت الله زاده شیرازی, ۱۴۰۰):
۱. ابتدا نظریه را بصورت گزاره‌نمایی به زبان منطق ارسطویی بازنویسی می‌کنیم.
۲. در گام بعدی، بررسی می‌شود که با فرض صادق از آب درآمدن گزارۀ نظریۀ مزبور، سور وجودی، چه موجوداتی را تحت پوشش قرار خواهد داد.
۳. دامنۀ سور وجودی، پس از مراحل الف و ب، همان تعهد هستی‌شناختی نظریه است.
می‌توان گفت که هر چیزی که وجود دارد یک متغیر است. عبارت مشهور کواین در مقاله‌ای باعنوان: در باب آنچه هست چنین است: «اینکه فرض کنیم چیزی موجود است، صرفاً به این معناست که آن چیز، ارزش یک متغیر است» (Quine, 1948). از آنجا که اصول منطق و استنتاج اغلب بر همگان آشکار است، در اینجا به چگونگی کسب معرفت در نظریۀ گراف‌ها که امروزه تاحدّ زیادی بر فلسفۀ اسپینوزا اِعمال شده است می‌پردازیم.
معرفت ریاضیاتی از طریق گراف
در روش کسب معرفت بواسطۀ گراف‌ها از روش مدل‌سازی ریاضیاتی استفاده می‌شود. مدل‌سازی به‌معنی انتقال از جهان واقعی به جهان مجرد ریاضی و سپس بکارگیری ابزار یا نظریه برای پیش‌بینی حقیقت است. دراینجا اگر یک موضوع یا پدیداری ازجهان ئاقعی را به‌منزلۀ یک سیستم در نظر بگیریم، آنگاه سیستم عبارت خواهد بود از مجموعه‌ای از اجزای مختلف که به یکدیگر وابسته و با هم مرتبط بوده و برای هدف خاص یا انجام کاری طراحی شده‌اند.
یک مدل ریاضی گراف با تعیین عناصر یک سیستم به‌منزلۀ رئوس و چگونگی ارتباط میان این عناصر، به‌منزلۀ یال‌ها، بصورت یک گراف شکل می‌گیرد. در شکل زیر، فرآیند مدل‌سازی گراف ارائه شده است:

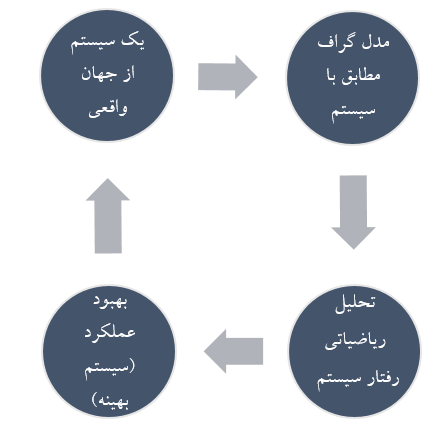
آنچه از مدل‌سازی گراف بدست می‌آید، بعلاوۀ استنتاجات منطق ارسطویی، اصل و پایۀ استدلال‌های اسپینوزا در کتاب اخلاق را تشکیل می‌دهد که اکنون به آن می‌پردازیم:

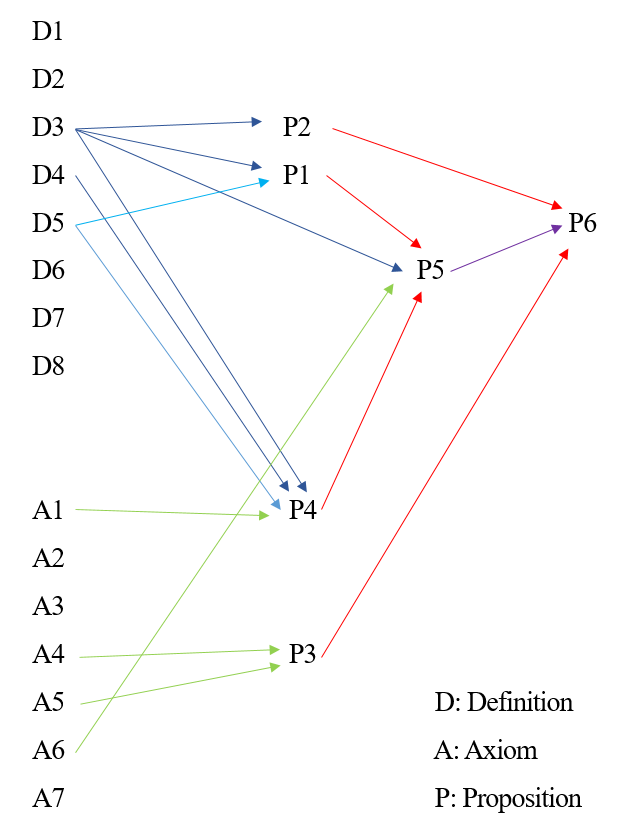
Definition = تعریف، Axiom = اصل متعارف، Proposition = قضیه

مبادی علم که مسائل بر آن متوقف‌اند عبارتند از: تعاریف، اصول متعارفه، و اصول موضوعه. تعاریف از نوع تصورات‌اند، تصورات معلوم که برای شناساندن ماهیات و امور مجهول بکار می‌روند. اصول متعارفه و اصول موضوعه، از نوع تصدیقات‌اند.
دربارۀ تعاریفی که اسپینوزا در کتاب اخلاق ارائه داده است شرحی از دکتر جهانگیری را در ذیل می‌آوریم:
«تعریف به اعتبار وجود معرف در خارج و عدم وجودش در آن، در دو مورد بکار می‌رود و درنتیجه به دو قسم تقسیم می‌شود:
۱. وجود شیء در خارج معلوم، اما ماهیتش مشکوک و نامعلوم است و لذا برای شناساندن و معلوم ساختن آن ماهیت به تعریف نیاز است.
۲. شیء در خارج موجود نیست، بلکه وجودش فقط در «فاهمه» و در مرحلۀ تصور است و لذا تعریف برای شناساندن ماهیت امری بکار می‌رود که بوسیلۀ ما تصور شده و یا ممکن است که به تصور درآید.» (اسپینوزا, ۱۳۹۹)
پس اینها تعاریفی است که اسپینوزا خود ارائه نموده است و اگر کسی بخواهد، ممکن است که این تعاریف را زیر سؤال برده و از این طریق نتایج و سیستم فلسفی او را به چالش بکشد. اما دربارۀ اصول متعارفه، باید گفت از آنجا که این اصول را گویا باید گزاره‌های ریاضیاتی مبنایی او در کسب معرفت ریاضیاتی دانست پس احتمالاً بدین معناست که جایی برای چالش و تردید نباید وجود داشته باشد. سپس، در مرحلۀ بعدی، اسپینوزا به روش استنتاج منطقی، از این گزاره‌های مبنایی به قضایای بیشتر و بیشتری استدلال کرده و شاکلۀ فلسفۀ خویش را استوار می‌نماید. (Autio, https://github.com/Autio, 2015)
ابتدا جهت آماده‌سازی ذهن و داشتن ایده‌ای ذهنی، استنتاجات منتج از صرفاً تعاریف را از نظر می‌گذرانیم (Autio, https://autio.github.io/, 2015):

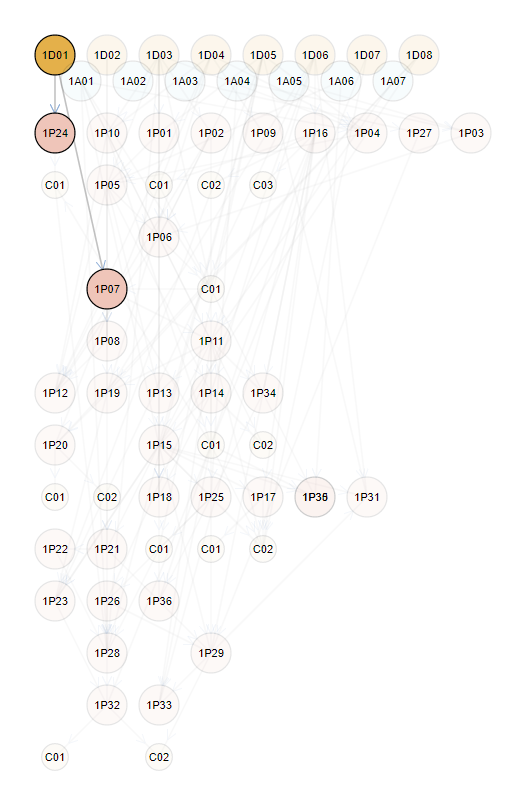
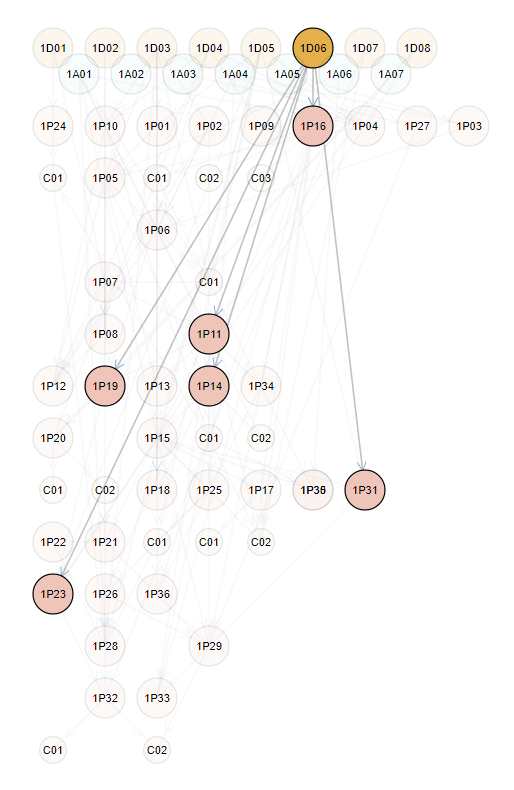
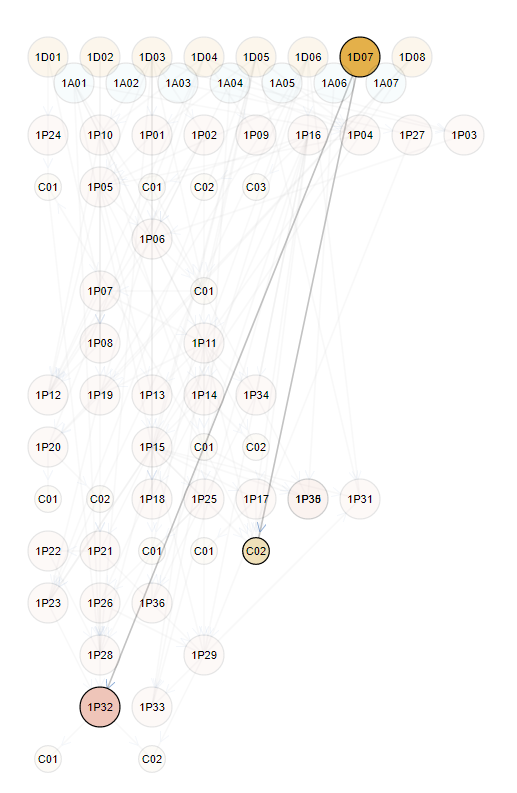
اکنون گراف‌های حاصل از استنتاجات فوق را در برخی منابع دیگر با هم مرور می‌کنیم (Pruss, 2011)

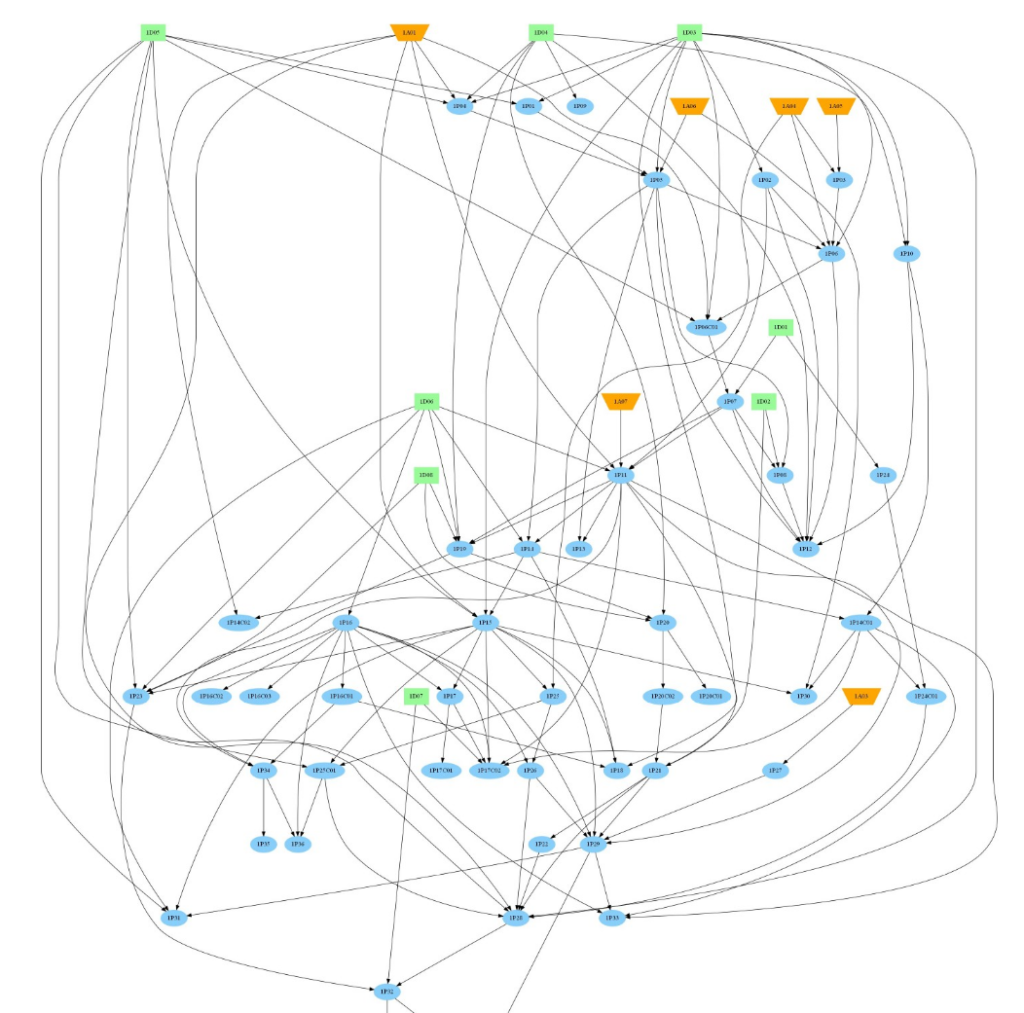
گراف حاصل از استنتاجات بخش اول رسالۀ اخلاق

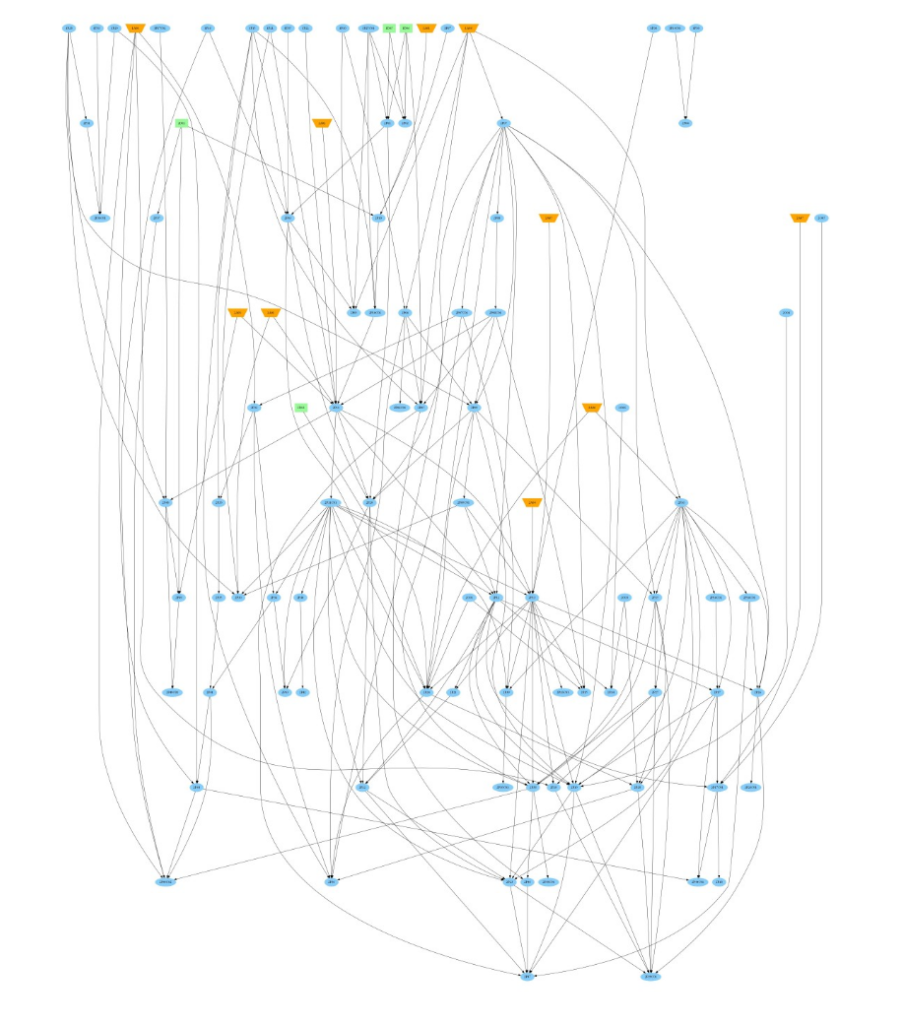
گراف حاصل از استنتاجات بخش دوم رسالۀ اخلاق

همچنین گراف‌های دیگری بر اساس فلسفۀ اسپینوزا در کتاب اخلاق طراحی و کار شده‌اند (Weinberg, 2018):

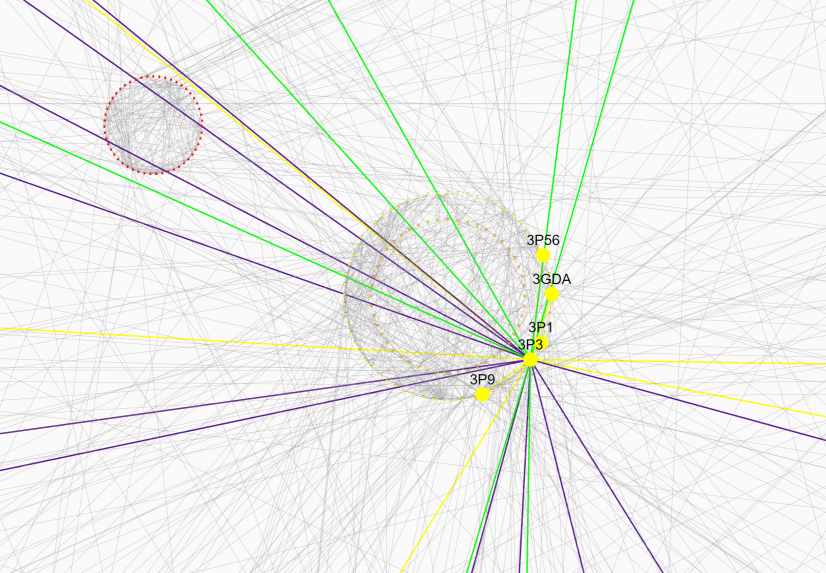
گراف‌های حاصل از هر پنج بخش رسالۀ اخلاق
این شکل کلی، در تصاویر بعدی با بزرگنمایی بهتر قابل درک خواهد بود

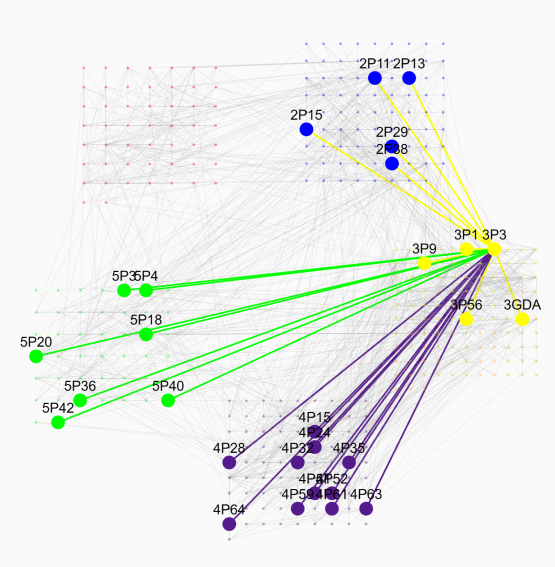
ارتباط میان گزاره‌های بخش‌های مختلف رسالۀ اخلاق

توضیح: عددی که قبل از حرف P نوشته شده است، نشان‌دهندۀ بخش مورد نظر در رسالۀ اخلاق می‌باشد. بعنوان مثال ۴P28 به‌معنی قضیۀ ۲۸ از بخش چهارم می‌باشد.

کتاب‌شناسی

.Autio, P. (2015). Retrieved from https://autio.github.io
.Autio, P. (2015). https://github.com/Autio
.Okrent, M. (1998). Being. Routledge
.Pruss, A. R. (2011). Spinoza graphs. Retrieved from http://alexanderpruss.blogspot.com
.Quine. (1948). On what there is. Review of Methaphysics, 21-38
.Weinberg, J. (2018). Digital Maps of Spinoza’s Ethics. Retrieved from https://dailynous.com

اسپینوزا, ب. (۱۳۹۹). اخلاق، ترجمۀ دکتر محسن جهانگیری. تهران: مرکز نشر دانشگاهی.
بابلیان, ا. (۱۳۸۶). مباحثی در ریاضیات گسسته. تهران: مبتکران.
سیدی فرد, س., & آیت الله زاده شیرازی, س. (۱۴۰۰). چگونه نظریۀ صادق‌ساز آرمسترانگ معیاری برای تعهد هستی شناختی است؟. متافیزیک.

https://www.mytutor.co.uk/answers/10942/A-Level/Philosophy/What-is-the-difference-between-determinism-and-fatalism/
https://github.com/Autio
https://prezi.com/h56665sj9jfk/spinozas/?frame=ccc32ae5e4d20a92bac23aa48770e2aabe92a511

منطق ریاضی؛ ویراست دوم

https://autio.github.io/projects/spinoza_ethics/